
Au fil des ans, les téléspectateurs de Channel 4 se sont branchés sur les gourous des mathématiques du compte à rebours, Carol Vorderman et Rachel Riley, qui nous ont posé des problèmes de mathématiques à couper le souffle. Mais certains des Compte à rebours les tours ont été résolus – quelque peu incroyablement – en quelques instants.
Super George
En octobre 2014, George a été chargé d’utiliser 1, 2, 25 et 100, ainsi que 75 et 50, pour arriver à 940.
George a réussi en faisant :
75 x 25 = 1875
Il a ensuite ajouté un pour 1876, avant de multiplier par 50 pour 93800, et de diviser par 100 pour donner 938, avant d’ajouter 2.
« Bien fait! » s’exclama Rachel Riley.
« Super George », a déclaré Nick Hewer.
« Où avons-nous trouvé ce type ? »
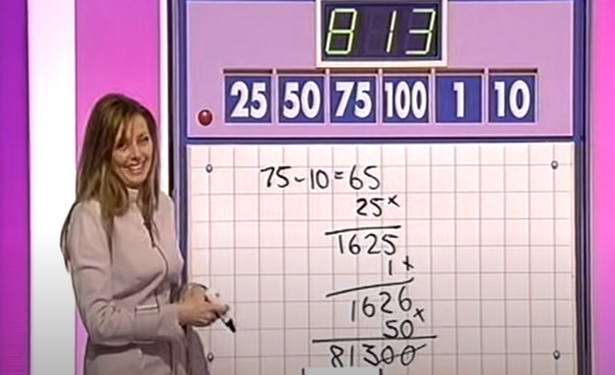
Pour obtenir 813, Carol a chargé deux candidats d’utiliser 1, 10, 25, 50, 75 et 100.
John a dit qu’il en avait 813, en utilisant :
75 – 10 = 65
65 x 25 = 1625
1625 + 1 = 1626
1626 x 50 = 81300
81300 divisé par 100 = 813
« Où avons-nous trouvé ce type ? demanda Richard Whiteley.



