

L’université d’Oxford (Image : Getty)
Si vous vous êtes déjà demandé si vous aviez l’intelligence d’étudier à Oxford, voici un avant-goût du processus de candidature. Ces questions ont toutes été envoyées aux personnes interrogées lors de l’admission, selon le Guardian, lors de la candidature à un diplôme de philosophie conjoint, alors préparez-vous à faire mal au cerveau après les avoir essayées et trouvez les réponses ci-dessous.
1. La surprise de Stéphanie
Stéphanie a invité ses amis Rowan et Colleen chez elle et elle leur dit qu’elle a une surprise cachée sous l’un des carrés bleus.
Il y a cependant un hic, Stephanie a dit en privé à Rowan le numéro de ligne de la surprise et à Colleen la lettre de colonne de la surprise. Tout le monde le sait, et la conversation s’engage :
Rowan : « Je ne sais pas où est la surprise, mais je sais aussi que Colleen ne le sait pas. »
Colleen : « Oui, en effet, au début je ne connaissais pas l’emplacement de la surprise. Mais maintenant je sais où il est.
Rowan : « Dans ce cas, je sais maintenant aussi où cela doit être. »
Question : Où pensez-vous que se trouve la surprise ?
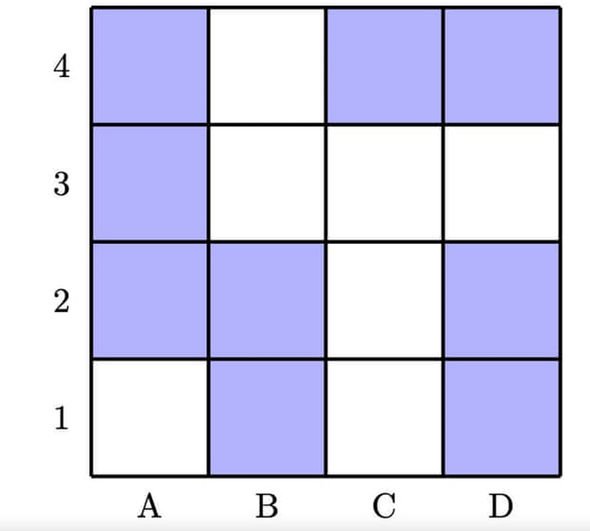
1. La surprise de Stéphanie (Image : Université d’Oxford)
2. Fête des tuiles
Lors d’une fête, Shelia et Colin tentent de trouver une surprise cachée sous les tuiles. Chaque ami est informé en privé d’une information sur l’endroit où se trouve la surprise.
Sheila connaît la forme du carreau.
Colin connaît la couleur du carreau.
Tout le monde sait que cela et aucune autre information n’est donnée.
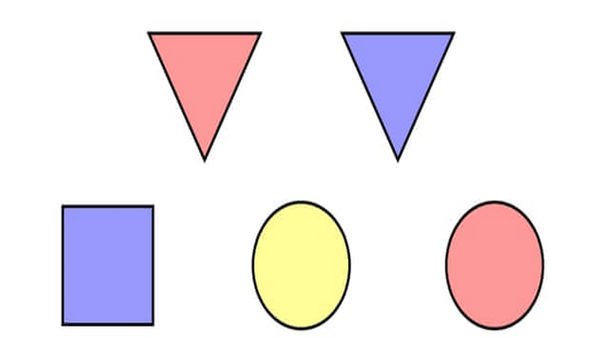
2. Fête des tuiles (Image : Université d’Oxford)
Animateur : « Est-ce que l’un de vous sait où est la surprise ? »
. . . Long silence gênant. . .
Animateur : « Le savez-vous maintenant ? »
. . . Plus de silence gênant. . .
Sheila, Colin : (simultanément) : « Maintenant, je sais où c’est ! »
Question : à votre avis, où est la surprise ?
3. Les boîtes d’Alice
Alice a invité ses amies Caroline et Susan chez elle et a placé plusieurs boîtes sur la table devant elles. Il y a une petite boîte rouge, une boîte rouge moyenne, une grande boîte noire, une petite boîte bleue et une grande boîte bleue.
Alice a dit à ses amis qu’elle avait mis un cadeau dans l’une de ces boîtes et a secrètement dit à Caroline la couleur de la boîte et à Susan la taille de la boîte – elles le savent toutes les deux.
Cette conversation suit :
Caroline : « Je ne sais pas quelle boîte contient le cadeau, et je sais aussi que Susan ne le sait pas. »
Susan : « Je savais déjà avant que vous ne parliez que vous ne saviez pas quelle boîte contient le cadeau. »
Caroline : « Ah, maintenant que tu dis ça, je me rends compte soudainement quelle boîte doit contenir le cadeau. »
Question : Quelle boîte contient réellement le cadeau ?

Avez-vous l’intelligence d’aller à l’Université d’Oxford ? (Image : Getty)
Ne comptez pas sur votre cerveau de maths alors que vous pourriez avoir un expert GRATUIT pendant 7 jours
Maths-Whizz est un professeur de mathématiques virtuel super intelligent qui propose des jeux, des leçons et des exercices interactifs pour les enfants de cinq à 13 ans.
Pour voir à quel point il est bon de transformer l’apprentissage à domicile pour les parents, nous avons négocié un prix exclusif de 20 % pour le rendre à 15,99 £ pour le premier mois.
Voyez si vous l’aimez d’abord et inscrivez-vous à un essai gratuit de 7 jours sans engagement en cliquant ici. Si vous souhaitez vous inscrire pour un mois à la fois ou même un an, tu peux faire c’est ici mais n’oubliez pas d’utiliser le code promo ‘MATHS20’.
Cet article contient des liens d’affiliation, nous pouvons recevoir une commission sur les ventes que nous en générons.
Ces questions visent toutes à révéler la personnalité d’un individu, sans parler de son raisonnement logique. Il s’agit de voir le processus se dérouler, pas seulement qui a raison et qui a tort. Elles sont toutes issues des questions d’entretien d’Oxford du célèbre philosophe mathématique Joel David Hamkins, elles sont donc très importantes.
Le Dr Tom Crawford, mathématicien à l’université, a déclaré: « Ces questions sont conçues pour tester votre pensée logique. Bien qu’elles puissent initialement sembler impénétrables, avec quelques conseils, j’espère que vous pourrez voir comment progresser vers la solution.
« Avec toute question d’admission, il est toujours important de se rappeler que pendant l’entretien, les candidats recevront des conseils et des astuces pour les orienter dans la bonne direction – ils ne sont pas censés pouvoir le faire immédiatement sans aucune aide. »
Et en parlant de conseils, Tom a ajouté : « Je trouve très utile de décomposer chaque énoncé pour déterminer exactement ce qu’il fait, ou ne fait pas, pour vous parler de la solution.
« Par exemple, sur la première question, puisque Rowan est informé de la ligne de la surprise mais dit qu’il ne connaît pas son emplacement, cela ne peut pas être la ligne trois. Ainsi, l’information que nous pouvons obtenir de cette première déclaration n’est pas la ligne trois ‘.
« Si vous adoptez une approche similaire pour toutes les autres affirmations, vous pouvez progressivement exclure de plus en plus de possibilités, vous laissant avec la bonne solution. »
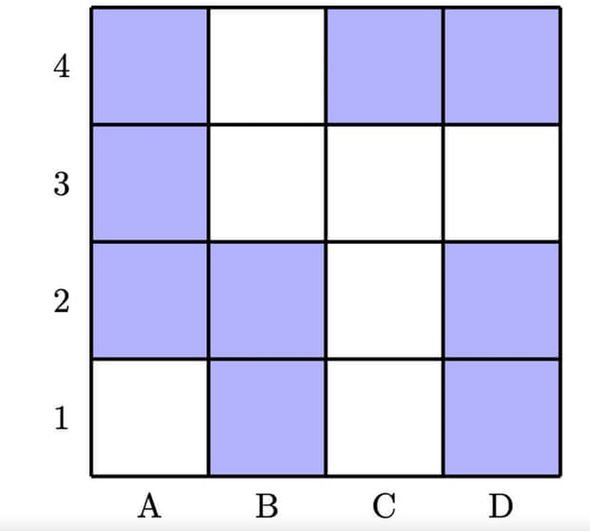
1. La surprise de Stéphanie (Image : Université d’Oxford)
Les réponses:
1. Sous le carré A2
Si Rowan ne sait pas où est la surprise, nous pouvons éliminer la ligne 3 (puisque si on lui disait la ligne 3, il connaîtrait la bonne case.) S’il sait que Colleen ne le sait pas, nous pouvons éliminer la ligne 4 (puisque la seule façon il serait possible pour Colleen de connaître la bonne case au début si c’était C4.) Si Colleen connaît maintenant la bonne case, elle doit connaître la colonne pour laquelle il ne reste qu’une seule option. Cette colonne est A, et donc le carré correct est A2.
2. Sous le triangle rouge
La seule façon pour Sheila de connaître la bonne tuile avant le dialogue est si on lui avait dit « carré », et la seule façon pour Colin de savoir c’est si on lui avait dit « jaune ». Puisqu’ils sont silencieux lorsque l’hôte pose la première question, nous supposons qu’ils ne connaissent pas la bonne tuile, et ainsi nous pouvons éliminer le carré et les tuiles jaunes. Si Sheila avait appris « cercle », elle connaîtrait maintenant la bonne tuile, car il ne reste qu’un seul cercle. Si Colin avait été dit « bleu », il connaîtrait également la bonne tuile. Cependant, étant donné que les deux restent silencieux lorsque l’hôte pose la deuxième question, nous pouvons supposer qu’ils ne connaissent pas la bonne tuile, et donc nous en déduisons que la tuile doit être rouge et un triangle.
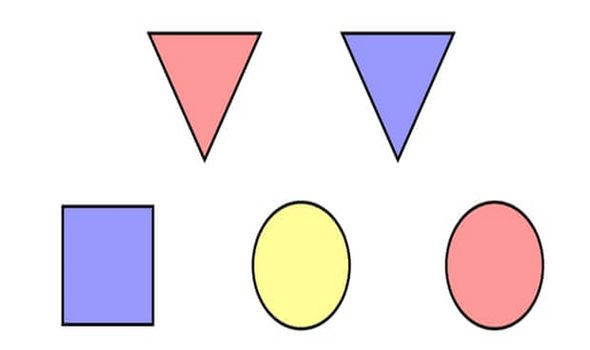
2. Fête des tuiles (Image : Université d’Oxford)
3. Petite boite bleue
Ce puzzle apparaît plus difficile car il n’y a pas d’illustration. Alors, pour vous faciliter la tâche, dessinez une grille 3×3 dans laquelle rouge, noir et bleu sont les colonnes et petites, moyennes et grandes les lignes. Les cases possibles, notées X, sont donc : XOX, XOO, OXX.
Si Caroline ne connaît pas la boîte, on ne peut pas lui avoir dit « noir ». Et si elle sait que Susan ne le sait pas, on ne peut pas dire à Caroline « rouge », car si on lui avait dit « rouge », il y a une chance qu’on lui ait dit « moyen », auquel cas Caroline ne le serait pas. capable de dire qu’elle sait que Susan ne sait pas. Donc, on en déduit que Caroline s’est fait dire « bleu ».
Maintenant, si, avant que Caroline ne parle, Susan savait que Caroline ne connaissait pas la bonne boîte, nous pouvons éliminer la possibilité qu’on lui ait dit « grande ». Puisque si on lui avait dit « grand », elle ne saurait pas avec certitude que Caroline ne le savait pas, puisqu’elle ne peut pas exclure la possibilité que la grande boîte noire ait le cadeau, auquel cas Caroline le saurait. Puisque la boîte est bleue et pas grande, la seule option restante est petite et bleue.
Comment t’es-tu entendu ? Faites le nous savoir dans les commentaires.



